01 - Números Complexos¶
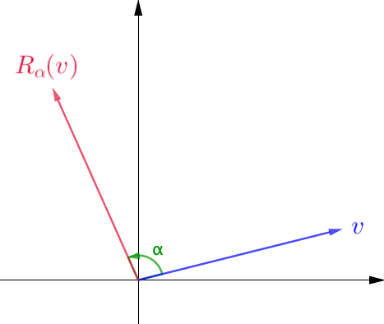
Em aula vimos a matriz que, quando aplicada a um vetor do plano (2D), realiza sua rotação de α radianos em torno da origem, no sentido anti-horário.
$$ R_\alpha = \begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} $$
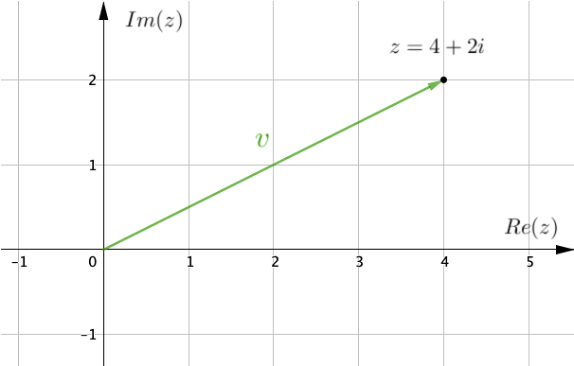
Nesta tarefa, você vai mostrar que essa rotação também pode ser feita por meio da multiplicação de números complexos, obtendo-se um resultado equivalente ao obtido com as matrizes. Para isso, vamos associar cada número complexo z=a+bi ao vetor v=(a,b), como ilustrado no plano complexo a abaixo.
- Considere os números complexos $z_1=4+2i$ e $z_2=i⋅z_1$.
a) Desenhe no plano complexo os vetores $v_1$ e $v_2$ que representam os números complexos $z_1$ e $z_2$, respectivamente.
b) Considere que seja aplicada ao vetor $v_1$ uma rotação de $α$ radianos em torno da origem, no sentido anti-horário. Usando a matriz de rotação vista em aula, determine, em função de $α$, as coordenadas do vetor obtido.
c) O vetor $v_2$ pode ser obtido por meio de uma rotação de $α$ radianos em torno da origem, no sentido anti-horário, aplicada ao vetor $v_1$. Usando a resposta ao item b, determine o valor de $α$ (em radianos, não esqueça!).
d) Determine o vetor $v_3$, obtido por meio da aplicação de uma rotação de $π/4$ radianos em torno da origem, no sentido anti-horário, ao vetor $v_1$.
e) Determine um número complexo $z$ tal que a multiplicação $z_1⋅z$ resulte em um número complexo $z_3$ cuja representação no plano complexo esteja associada ao vetor $v_3$.
No exercício 1, você realizou a rotação de alguns vetores por meio da matriz de rotação e também usando a multiplicação de números complexos. No entanto, ainda não generalizou a segunda estratégia, ou seja, ainda não estabeleceu o número complexo que deve ser multiplicado para que se obtenha uma rotação desejada. Faremos isso no exercício 2.
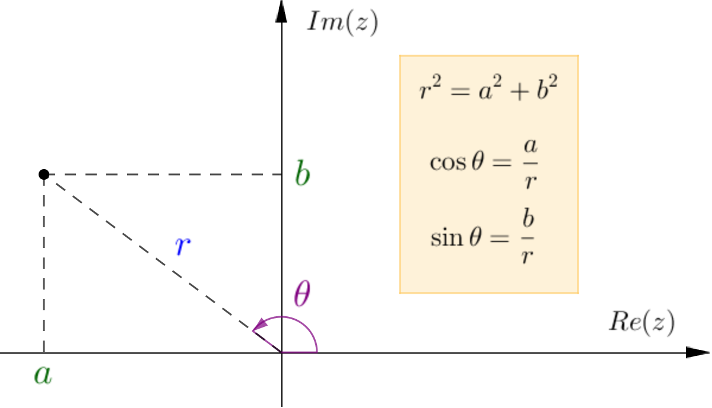
- Todo número complexo pode ser escrito na forma algébrica $(z=a+bi, com a,b∈R)$ ou na forma trigonométrica $(z=r(cosθ+isenθ)$, sendo $r$ o módulo e $θ$ o argumento do número complexo).
Represente, na forma trigonométrica, os números complexos $z_1=1$, $z_2=3i$, $z_3=1+i$, $z_4=-1-i√3$ e $z_5=-√2/2+i √2/2$.
b) Na forma trigonométrica, é muito prático multiplicar dois números complexos. Sendo $z_1=r_1 (cosθ_1+isenθ_1)$ e $z_2=r_2 (cosθ_2+isenθ_2)$, temos que:
$$ z_1⋅z_2=r_1⋅r_2⋅(cos(θ_1+θ_2 )+isen(θ_1+θ_2 )) $$
Em outras palavras, basta multiplicar os módulos e somar os argumentos. Dado um número complexo $z$, representado no plano complexo por um vetor $v$, determine um número complexo $z_θ$ tal que o produto $z⋅z_θ$ seja representado por um vetor $v_θ$ que corresponda à rotação de θ radianos do vetor v em torno da origem, no sentido anti-horário. Justifique sua resposta (um desenho pode ajudar!).
Dica: lembre-se de que um vetor não tem o seu módulo alterado quando é submetido a uma rotação.